Antenna Designer

Assume an antenna under test (AUT) is far enough from the chamber walls that the wall reflections can be ignored. Define a near-field scaling factor, k, so the measurement distance = 2*D**2*k/wavelength. The approximate quadratic phase factor of the measurement is S = 1/(16*k). Compute the aperture diameter or width in wavelengths: DW=D/wavelength, the equivalent k factor used below can be increased by the factor: Sqrt(1 + (1/(4*k*DW))**2) for more accurate results, but for most apertures this factor is nearly one.
 
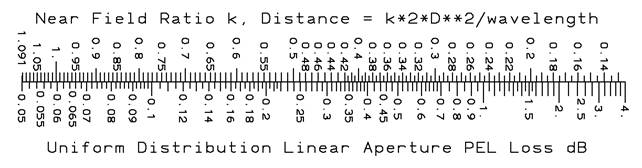
Much smaller k than given on the scale soon produce a pattern dip on axis and should not be used with a uniform distribution.

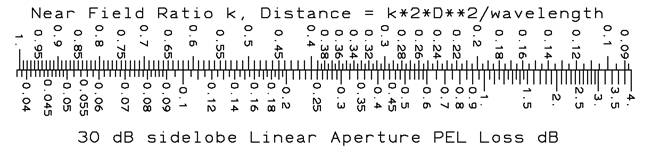
A rectangular aperture antenna with near field ratios k(e) and k(h) in the principal planes would have a total measurement loss given by the sum of the values for each plane given by the scales above.

Additional loss occurs due to the extra taper loss across the aperture, but it is small and can be ignored in most cases. The pattern of the chamber feed horn increases the amplitude taper across the antenna depending on its beamwidth. The pattern angle of the feed is related to the near field ratio k and the aperture width in wavelengths DW
Feed Angle = acos(1/sqrt(1+ 1/(2*k*DW)**2)
There is additional taper loss due to the path distance to the edge relative to the aperture center:
taper (dB) = 10*Log(1+1/(2*k*DW)**2)
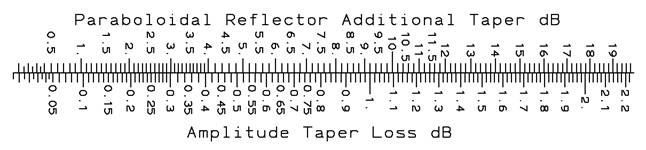
We sum the tapers due to the feed pattern and path length ratio and consider the amplitude taper losses to the AUT. For a paraboloidal reflector the taper loss is given by the scale.

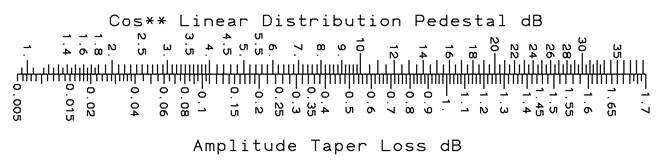
A linear antenna’s taper can be approximated by a cosine squared on a pedestal distribution where the 30 dB sidelobe antenna has a 13 dB taper. Use the scale below and subtract the loss for a 13 dB taper from the total loss now across the antenna due to the taper for a low sidelobe antenna while a nearly uniform distribution uses the scale without adjustment. Of course, the near-field measurement eliminates pattern nulls and raises sidelobe levels.